For
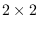
matrices over commutative rings, we prove a
characterization theorem for left stable range 1 elements, we show
that the stable range 1 property is left-right symmetric (also) at
element level and we show that all matrices with one zero row (or
zero column) over Bézout rings have stable range 1. Using
diagonal reduction, we characterize all the
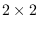
integral
matrices which have stable range 1 and discuss additional properties
including Jacobson's Lemma for stable range 1 elements. Finally, we
give an example of exchange stable range 1 integral
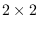
matrix which is not clean.
matrix.