In this paper, we establish some new sufficient conditions for oscillation
of the third order nonlinear functional dynamic equation
on a time scale
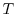
, where
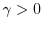
is the quotient of odd
positive integers,
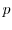
,
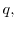
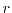
and
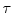
are positive rd-continuous
functions defined on
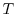
and
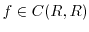
,
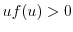
and

for
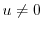
.
The results provided substantial improvement over those obtained by Yu and
Wang [J. Comp. Appl. Math. 225 (2009), 531-540] and Hassan [Oscillation of
third order nonlinear delay dynamic equations on time scales, Math. Comp.
Modelling 49 (2009), 1573-1586], in the sense that our results can be
applied when
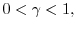
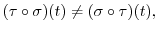
and do not require that
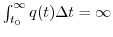
.
Some examples illustrating the main results are given.