Constantin Buse and Manuela-Suzy Prajea: Asymptotic behavior of discrete and continuous semigroups on Hilbert spaces, p.123-135

Abstract:

Let $\phi:[0,\infty)\rightarrow\lbrack0,\infty)$ be a nondecreasing function with $\phi(t)>0$ for all $t>0,$ $H$ be a complex Hilbert space and let $T$ be a bounded linear operator acting on $H.$ Among our results is the fact that $T$ is power stable (i.e. its spectral radius is less than $1)$ if

$$\sum_{n=0}^{\infty}\phi(\vert\langle T^{n}x,x\rangle\vert)<\infty$$

for all $x\in H$ with $\vert\vert x\vert\vert\leq1.$

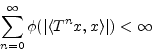
In the continuous case we prove that a strongly continuous uniformly bounded semigroup of operators acting on a Hilbert space $H$ is spectrally stable (i.e. the spectrum of its infinitesimal generator lies in the open left half plane) if and only if for each $x\in H$ and each $\mu\in\mathbb{R}$ one has:

$$\sup\limits_{s\geq0}\left\vert \int\nolimits_{0}^{s}e^{-i\mu t}\langle T(t)x,x\rangle dt\right\vert <\infty.$$

Key Words: Spectral radius, discrete semigroups, strongly continuous semigroups, uniform exponential stability, Orlicz space.

2000 Mathematics Subject Classification: Primary: 47D03,
Secondary: 11M35.

Download the paper in pdf format here.