Hugo Corrales and Carlos E. Valencia: On the critical group of matrices. p.213-236

Abstract:

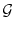
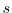
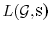
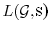
Given a graph $\mathcal{G}$ with a distinguished vertex $s$, the critical group of $(\mathcal{G},s)$ is the cokernel of their reduced Laplacian matrix $L(\mathcal{G},s)$. In this article we generalize the concept of the critical group to the cokernel of any matrix with entries in a commutative ring with identity. In this article we find diagonal matrices that are equivalent to some matrices that generalize the reduced Laplacian matrix of the path, the cycle, and the complete graph over an arbitrary commutative ring with identity. We are mainly interested in those cases when the base ring is the ring of integers and some subrings of matrices. 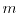Using these equivalent diagonal matrices we calculate the critical group of the $m$-cones of the $l$-duplications of the path, the cycle, and the complete graph. 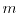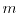Also, as byproduct, we calculate the critical group of another matrices, as the $m$-cones of the $l$-duplication of the bipartite complete graph with $m$ vertices in each partition and the bipartite complete graph with $2m$ vertices minus a matching.

Key Words: Critical group, matrices, cartesian product, complete graph, path, cycle.

2000 Mathematics Subject Classification: Primary: 05C25;
Secondary: 05C50, 05E99.

Download the paper in pdf format here.