Aurelian Gheondea: When are the products of normal operators normal?, p.129-150

Abstract:

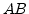
Given two normal operators $A$ and $B$ on a Hilbert space it is known that, in general, $AB$ is not normal. The question on characterizing those pairs of normal operators for which their products are normal has been solved for finite dimensional spaces by F.R. Gantmaher and M.G. Krein in 1930, and for compact normal operators by N.A. Wiegmann in 1949. 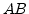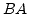Actually, in the afore mentioned cases, the normality of $AB$ is equivalent with that of $BA$, and a more general result of F. 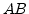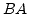Kittaneh implies that it is sufficient that $AB$ be normal and compact to obtain that $BA$ is the same. On the other hand, I. 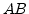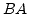Kaplansky had shown that it may be possible that $AB$ is normal while $BA$ is not. 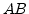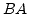When no compactness assumption is made, but both of $AB$ and $BA$ are supposed to be normal, the Gantmaher-Krein-Wiegmann Theorem can be extended by means of the spectral theory of normal operators in the von Neumann's direct integral representation.

Key Words: Normal operator, compact operator, product, singular numbers, direct integral Hilbert space, decomposable operator.

2000 Mathematics Subject Classification: Primary: 47B15,
Secondary: 46L10.

Download the paper in pdf format here.